錯誤更正碼
此條目可參照英語維基百科相應條目來擴充。 (2019年8月29日) |
在電腦,電信,資訊理論和編碼理論中,錯誤更正碼(ECC,error correction/correcting code)是資訊傳輸中錯誤檢測與糾正的工具。它通常用在不可靠或嘈雜的頻道中。[1][2]資料傳送方利用錯誤更正碼中的冗餘資訊,使得接收方能夠檢測訊息傳輸中發生的錯誤,而且通常可以糾正這些錯誤而無需重新傳輸。美國數學家理察·漢明(Richard Hamming)在1940年代開創了這一領域,並在1950年發明了第一個錯誤更正碼:漢明(7,4)代碼。[2]
相比錯誤檢測,錯誤更正碼不僅能夠檢測到錯誤,而且可以將其更正。它的優點是在出現錯誤時不需要反向頻道來請求重發資料,缺點是訊息中增加了固定開銷,因此需要更高的前向頻道頻寬。因此,錯誤更正碼用於重傳成本高昂或無法實現的情況,例如單向通訊鏈路,時延較長的連結,以及以多播方式傳送給多個接收者的連結。比如,繞天王星執行的衛星,由於傳輸錯誤而造成的重發會造成5個小時的延遲。錯誤更正碼資訊通常添加到大容量儲存裝置中,以恢復損壞的資料,並廣泛用於數據機、固態硬碟,以及主記憶體為 ECC 主記憶體的系統中。
接收機中的錯誤更正碼處理可以應用於數位位元流,也可以應用於數位調變載波的解調。對於後者,錯誤更正碼是接收器中類比數位轉換器的組成部分。維特比(Viterbi)解碼器採用軟判決演算法,以從被雜訊破壞的類比訊號中解調數位資料。許多錯誤更正碼編碼器/解碼器還可以生成位元錯誤率(BER)訊號,該訊號可用作回饋以微調類比接收電子裝置。
錯誤更正碼能夠糾正的錯誤位/遺失位的最大數量取決於它的的設計,因此,不同的錯誤更正碼適用於不同的環境。一般來說,能夠糾正大量錯誤的代碼中有著更多的冗餘資訊,所以會需要更多頻寬進行傳輸,從而降低了有效位元速率,且同時提高了接收到的有效訊號雜訊比。克勞德·夏農(Claude Shannon)的有噪頻道編碼定理回答了以下問題:若使用最有效的代碼將解碼錯誤概率變為零,資料通訊還剩下多少頻寬?對於具有基本雜訊水平的頻道,該定理給出了理論上的最大資訊傳輸速率。但是,該證明不具建設性,也就是說它並不能用來構建實現最大速率的代碼。經過多年的研究,如今[何時?]一些先進的錯誤更正碼系統,其速率已非常接近理論最大值。
工作原理
[編輯]錯誤更正碼的編碼方法如下:發信方利用演算法,向要傳輸的資訊添加冗餘位。這些冗餘位通常是將原始輸入位由複雜的函式轉換而成。原始資訊不一定原樣出現在輸出的編碼中;包含原始資訊的代碼稱為系統代碼,反之稱為非系統代碼。
下面是一個簡單錯誤更正碼的例子:將每個資料位傳送3次。這種編碼稱為(3,1)重複碼。 通過嘈雜的頻道,接收器可能會收到8個不同版本的輸出,參見下表:
| 接收訊號 | 解碼 |
|---|---|
| 000 | 0 (無錯) |
| 001 | 0 |
| 010 | 0 |
| 100 | 0 |
| 111 | 1 (無錯) |
| 110 | 1 |
| 101 | 1 |
| 011 | 1 |
若收到的資訊非3個重複的數位,則以重複次數較多的數位為準。該錯誤更正碼最多糾正一位錯誤位,或兩位遺失位。雖然這種錯誤更正碼實施方便且應用廣泛,但這種三重模組冗餘的形式是效率較低的。更好的錯誤更正碼通常會檢查先前接收到的幾十位,或幾百位,由此判斷如何解碼當前的幾位(通常以2到8位元為一組)。
利用雜訊的「平均化」來減少錯誤
[編輯]錯誤更正碼的使用對資訊雜訊產生的破壞有「平均化」的作用。由於每一個原始資料位生成了多於一個的傳輸符,儘管某些傳輸符可能遭到雜訊的破壞,接收方通常能夠依賴其它未損壞的,由相同原始位生成的接收符來取得原本資料。由於這種效應,使用錯誤更正碼的數位通訊系統往往能夠在訊號雜訊比遠高於最小訊號雜訊比的情況下運轉。在運轉過程中,系統的訊號雜訊比永遠不會低於最小訊號雜訊比。當使用更強的,接近夏農極限的代碼時,這種懸崖效應將變得更加明顯。有時,頻道錯誤通常是突發型的。在這種情況下,可以使用交錯的錯誤更正碼來將資料編碼,這樣能夠降低所傳輸錯誤更正碼的懸崖效應。但是,這種方法也有局限性,它比較適用於窄頻資料。
大多數電信系統使用固定的頻道代碼,這樣的頻道代碼通常可以容忍預期的最壞誤碼率;如果誤碼率高於該值,則系統根本無法運轉。但是,有些系統能夠適應特定的頻道錯誤條件:在一些混合式自動重送請求的實例中,錯誤率較低時系統使用固定的錯誤更正碼,而在錯誤率過高時切換到自動重傳請求。 自適應調變和編碼能夠應對多種錯誤率:當通道中的錯誤率較高時,在每個封包中添加更多的糾錯位,而在不需要它們時將其刪除。
錯誤更正碼的種類
[編輯]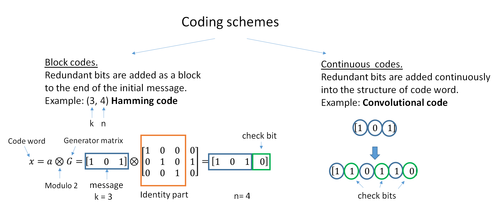
區塊碼適用於一連串固定長度的封包,而每一種區塊碼只能用於特定長度的封包。實際用途中的區塊碼一般使用硬解碼方式,所需時間為每一個封包長度的多項式時間。區塊碼有許多不同的類型,值得關注的有里德-所羅門碼,它被廣泛的應用於光碟,DVD和硬碟機中。經典區塊碼的其他例子有格雷碼,BCH碼,多維奇偶校驗碼和漢明碼。
卷積碼適用於任意長度的位元流/符號流。接收方通常使用維特比演算法將其軟解碼,但有時也會用其他演算法。隨著卷積碼約束條件的長度增加,維特比解碼的解碼效率漸近最佳;但作為代價,計算時間將以對數式增長。長度有限的卷積碼也可以看作一種「區塊碼」,因為輸入資料是成組的;但是卷積碼的每一「組」長度不一,而區塊碼的長度是固定的,且由其特定的代數性質而定。 卷積碼有幾種不同的終止方式,如「咬尾巴(tail-biting)」和「位元重新整理(bit-flushing)」。
漢明錯誤更正碼一般用來糾正NAND快閃記憶體錯誤[3]。它可以矯正一位錯誤或檢測兩位錯誤。漢明碼僅適用於相對可靠的單層單元NAND,較稠密的多層單元NAND需要能夠校正更多位的錯誤更正碼,例如BCH或里德-所羅門碼[4][5] 。NOR快閃記憶體通常不需要任何錯誤校正。[4]
區塊碼通常使用硬決策演算法解碼[6],在這種決策方式下,每個輸入和輸出訊號都非1即0。而卷積碼則相反,使用如維特比,MAP或BCJR演算法之類的軟決策演算法進行解碼,該演算法用於離散化的類比訊號,並且比硬判決解碼具有更高的糾錯效能。
幾乎所有的經典區塊碼都利用了有限域的代數性質。因此,經典區塊碼也稱為代數位。
經典區塊碼的檢錯或糾錯能力通常是事先預定的,而許多現代的區塊碼(例如低密度奇偶檢查碼)並沒有這方面的保證;它們的能力是由誤碼率來評估的。
大多數前向錯誤更正碼僅糾正翻轉位,而不能糾正插入位或遺失位。在這種情況下,計算誤碼率時應使用漢明距離。一些前向錯誤更正碼可以糾正插入位和遺失位,例如標記碼和浮水印碼。若使用此類代碼,測量位元錯誤率時使用萊文斯坦距離更加合適。 [7]
可靠性和編位元速率的權衡利弊
[編輯]錯誤更正碼的基本原理是以添加冗餘位的方法,來幫助解碼器尋回編碼前的原本訊息。錯誤更正碼系統的編位元速率指的是通訊包中,資訊位數與總位數(總位數=資訊+冗餘位數)之間的比率。接近零的低位元速率表示代碼的糾錯能力強,反之,若錯誤更正碼有著接近1的大位元速率,則意味著代碼的糾錯能力較弱。
傳輸這些冗餘位時,必須消耗有限的通訊資源,這導致了可靠性和資料速率之間的相互衝突[8]。在極端情況下,具有低傳輸效率的強代碼會導致接收器訊號雜訊比的大幅增加,這樣降低了誤碼率,但同時也降低了有效資料的速率。另一方面,不使用任何錯誤更正碼(此時位元速率=1)將整個頻道用於資訊傳輸目的,這樣效率極高但沒有任何糾錯能力。
具有極低錯誤率的錯誤更正碼,能夠達到怎樣的資訊傳輸效率?克勞德·夏農的第二定理給出了答案,根據該定理,若錯誤率趨於零,錯誤更正碼的速率最大可以達到頻道容量[9] 。他的證明使用了高斯隨機編碼,並不適用於實際應用。夏農給出了一個速率的上限,而學界為了設計出達到速率上限的錯誤更正碼,踏上了漫長的旅途。如今,有些錯誤更正碼幾乎可以達到夏農極限,但是通常實施起來極其複雜。
常見的幾種錯誤更正碼必須在糾錯效能和計算複雜度之間取得平衡。通常,它們的參數可以適用特定區間以內的編位元速率,可以根據不同的情況自動選擇較優的編位元速率。這樣可以降低冗餘位對資料速率的影響,同時減少錯誤。最佳化編位元速率的另一個準則是在低誤碼率的情況下儘量減少重傳次數,以降低通訊的能源成本。[10]
如上文中的許多例子所示,「不定式」一詞並不表明它的極限不存在。在許多情況下,我們可以使用洛必達法則,代數方程求解,或其他方法計算極限。
錯誤更正碼列表
[編輯]| Distance | Code |
|---|---|
| 2 (單錯誤檢測) | 奇偶性 |
| 3 (單錯誤檢測) | 三重模組冗餘 |
| 3 (單錯誤檢測) | perfect Hamming such as Hamming(7,4) |
| 4 (SECDED) | Extended Hamming |
| 5 (雙重錯誤校正) | |
| 6 (雙重錯誤校正/三重錯誤檢測) | |
| 7 (三錯誤校正) | perfect binary Golay code |
| 8 (TECFED) | extended binary Golay code |
- AN codes
- BCH碼,可以設計為更正每個代碼塊中任意數量的錯誤。
- 伯格碼
- Constant-weight code
- 卷積碼
- Expander code
- Group code
- Golay code
- Goppa code, used in the McEliece cryptosystem
- Hadamard code
- Hagelbarger code
- 漢明碼
- 基於拉丁方陣的代碼
- Lexicographic code
- Long code
- 低密度奇偶檢查碼
- 盧比變換碼
- m of n codes
- Online code
- 極化碼
- Raptor code
- 里德-所羅門碼
- Reed–Muller code
- Repeat-accumulate code
- Repetition code
- 脊柱代碼,一種基於偽隨機雜湊函式的無速率非線性代碼。[11]
- Tornado code
- 渦輪碼
- Walsh–Hadamard code
- 循環冗餘校驗
另見
[編輯]參考文獻
[編輯]- ^ Glover, Neal; Dudley, Trent. Practical Error Correction Design For Engineers Revision 1.1, 2nd. CO, USA: Cirrus Logic. 1990. ISBN 0-927239-00-0. ISBN 978-0-927239-00-4.
- ^ 2.0 2.1 Hamming, R. W. Error Detecting and Error Correcting Codes. Bell System Technical Journal (USA: AT&T). April 1950, 29 (2): 147–160. doi:10.1002/j.1538-7305.1950.tb00463.x.
- ^ "Hamming codes for NAND flash memory devices" (頁面存檔備份,存於網際網路檔案館). EE Times-Asia. Apparently based on "Micron Technical Note TN-29-08: Hamming Codes for NAND Flash Memory Devices" (頁面存檔備份,存於網際網路檔案館). 2005. Both say: "The Hamming algorithm is an industry-accepted method for error detection and correction in many SLC NAND flash-based applications."
- ^ 4.0 4.1 What Types of ECC Should Be Used on Flash Memory? (Application note). Spansion. 2011 [2020-06-26]. (原始內容存檔 (PDF)於2016-03-04).
Both Reed-Solomon algorithm and BCH algorithm are common ECC choices for MLC NAND flash. ... Hamming based block codes are the most commonly used ECC for SLC.... both Reed-Solomon and BCH are able to handle multiple errors and are widely used on MLC flash.
|url-status=和|dead-url=只需其一 (幫助) - ^ Jim Cooke. The Inconvenient Truths of NAND Flash Memory (PDF): 28. August 2007 [2020-06-26]. (原始內容存檔 (PDF)於2020-11-12).
For SLC, a code with a correction threshold of 1 is sufficient. t=4 required ... for MLC.
- ^ Baldi, M.; Chiaraluce, F. A Simple Scheme for Belief Propagation Decoding of BCH and RS Codes in Multimedia Transmissions. International Journal of Digital Multimedia Broadcasting. 2008, 2008: 1–12 [2020-06-26]. doi:10.1155/2008/957846
 . (原始內容存檔於2019-12-18).
. (原始內容存檔於2019-12-18).
- ^ Shah, Gaurav; Molina, Andres; Blaze, Matt. Keyboards and covert channels. USENIX. 2006 [20 December 2018]. (原始內容存檔於2021-03-08).
- ^ Tse, David; Viswanath, Pramod, Fundamentals of Wireless Communication, Cambridge University Press, UK, 2005
- ^ Shannon, C. E. A mathematical theory of communication (PDF). Bell System Technical Journal. 1948, 27 (3–4): 379–423 & 623–656 [2021-07-20]. doi:10.1002/j.1538-7305.1948.tb01338.x. hdl:11858/00-001M-0000-002C-4314-2
 . (原始內容存檔 (PDF)於2022-02-12).
. (原始內容存檔 (PDF)於2022-02-12).
- ^ Rosas, F.; Brante, G.; Souza, R. D.; Oberli, C. Optimizing the code rate for achieving energy-efficient wireless communications. Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC). 2014 [2021-07-20]. (原始內容存檔於2021-07-20).
- ^ Perry, Jonathan; Balakrishnan, Hari; Shah, Devavrat. Rateless Spinal Codes. Proceedings of the 10th ACM Workshop on Hot Topics in Networks. 2011. doi:10.1145/2070562.2070568.
